前言

        在算法中，递推是一种重要的方法。通过列出递推式，我们可以解决许多棘手的问题。

“状态”

        在算法中，状态是指某个变量在某种特定情况下的值。例如当i>=0时，abs(i)==i；而当i<=0时，abs(i)==-i。如果我们把这里的abs(i)赋值给一个变量j，那么这个变量j的状态（值）就随着i的变化而变化。

        就上面这个例子，我们可以列出关于j的状态转移方程：当i>=0时，j[i]=i；当i<=j时，j[i]=-i。

程序设计思路

        在解决具有嵌套性质的问题时，尤其是当n的值不同，且各个答案之间有关联的问题时，列出一个正确的递推式，就几乎等于解决了问题，不必进行暴力搜索等操作。

        由于直接讲解比较抽象，所以我们直接来看题目。

代码实现

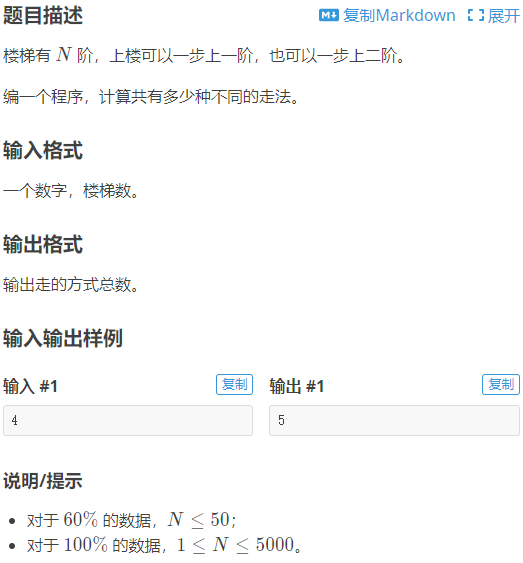
        可以看到，这道题要求我们计算走楼梯的步数。很显然，如果我们使用搜索来解题，那么速度将会偏慢，导致TLE。所以，这里我们使用递推来解决问题。

        由题意，可知走到第x个台阶，一定是从第i-1个台阶或从第i-2个台阶出发。由此，我们可以列出方程：f[x]=f[x-1]+f[x-2]（f[x]表示走到第x个台阶的方案总数）。

        列出方程后，我们只需要找到这个方程的初始状态就可以求解了。而不难看出f[1]=1，f[2]=2。问题解决！

        你以为这就完了？No！注意数据没有范围，要用高精度！！！（如果不知道怎么用高精度的可参考：https://blog.faryou.eu.org/post/98.html）

        代码如下：

#include <bits/stdc++.h>
using namespace std;

int a[5010][5000],len=1,n;//a相当于上文中的f（高精度所以用二维），len存储位数，n见题意

void add(int arr){
	for(int i=1;i<=len;i++) a[arr][i]=a[arr-1][i]+a[arr-2][i];//高精度一位一位加
	for(int i=1;i<=len;i++) if(a[arr][i]>=10){//进位
		a[arr][i+1]+=a[arr][i]/10;
		a[arr][i]%=10;
	}
	if(a[arr][len+1]>0) len++;//位数++
	return ;
}

int main(){
	scanf("%d",&n);
	a[0][1]=1;//初始值，因为f[2]=2=f[1]+1
	a[1][1]=1;
	for(int i=2;i<=n;i++) add(i);//重复计算
	for(int i=len;i>0;i--) printf("%d",a[n][i]);
	return 0;
}

结语

        递推是一个极为重要的方法，后面要学习的DP（动态规划）本质上就是分类讨论列出不同情况下的状态转移方程。我是faryou，下次见！

本文链接：https://blog.faryou.eu.org/post/104.html 转载需经作者授权！