前言

        通常情况下，我们在编程过程中，int的数据范围已经足够我们使用。如果数据较大，可以使用long long型数据。但在某些特殊场景下，这些数据都已经无法满足我们的需求。这时，我们就需要高精度。

程序设计思路

        高精度的基本思路就是小学竖式计算，因此，我们需要一个数组，其中一个变量存下一个数位。而为了输入方便，我们使用字符串存储数据。

        由于C++的某些特性，我们需要把低位存放在数组低位，高位存储在数组高位。故需要倒序存放。

代码实现

        首先来看高精度的原始代码：

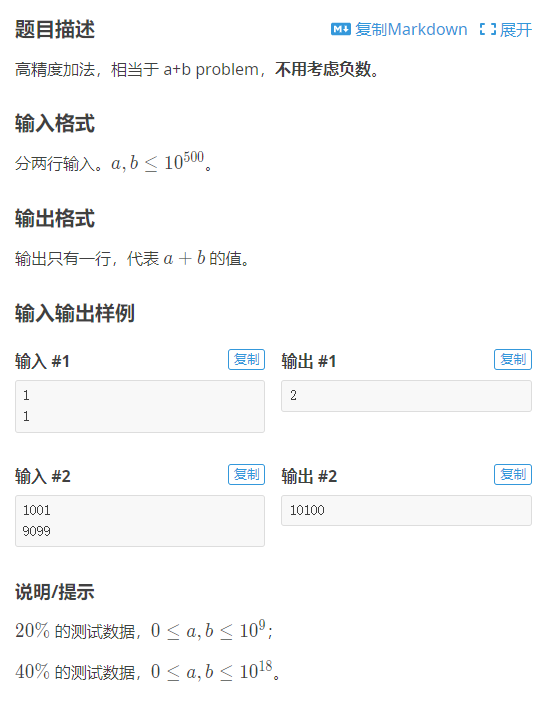
//个人喜欢使用C风格，因此用了char数组存字符串，如果你喜欢C++的STL，也可以用string
#include <bits/stdc++.h>
using namespace std;

bool p=false;//记录结果位数是否吧加数中大者多一位
int iq[4][2000],len,lena=0,lenb=0;//iq存加数及结果，len为加数中较大者位数，lena、lenb分别为a、b的长度
char a[1000],b[1000];//用于输入的字符串
int main(){
  scanf("%s%s",&a,&b);//读入
  //变量初始化
  for(int i=0;i<2000;i++) iq[1][i]=0;
  for(int i=0;i<2000;i++) iq[2][i]=0;
  for(int i=0;i<2000;i++) iq[3][i]=0;
  //取位数
  lena=strlen(a);
  lenb=strlen(b);
  //字符串转数组
  for(int i=0;i<=lena-1;i++) iq[1][i]=a[lena-i-1]-'0';
  for(int i=0;i<=lenb-1;i++) iq[2][i]=b[lenb-i-1]-'0';
  //取加数中位数多者作为结果位数
  len=max(lena,lenb);
  //将数组中对应为相加
  for(int i=0;i<len;i++) iq[3][i]=iq[1][i]+iq[2][i];
  //进位
  for(int i=0;i<len-1;i++) if(iq[3][i]>=10){
    iq[3][i]%=10;
    iq[3][i+1]++;
  }
  //处理最高位进位
  if(iq[3][len-1]>=10){
    iq[3][len-1]%=10;
    iq[3][len]++;
    p=true;
  }
  //先输出最高位（如果有）
  if(p) printf("%d",iq[3][len]);
  //由于倒序存储，倒序输出
  for(int i=len-1;i>=0;i--) printf("%d",iq[3][i]);
  return 0;
}

        可以看到，这里的思路非常清晰，即对两数进行竖式计算。下面来看一个把高精度嵌入正常应用的简单例子：

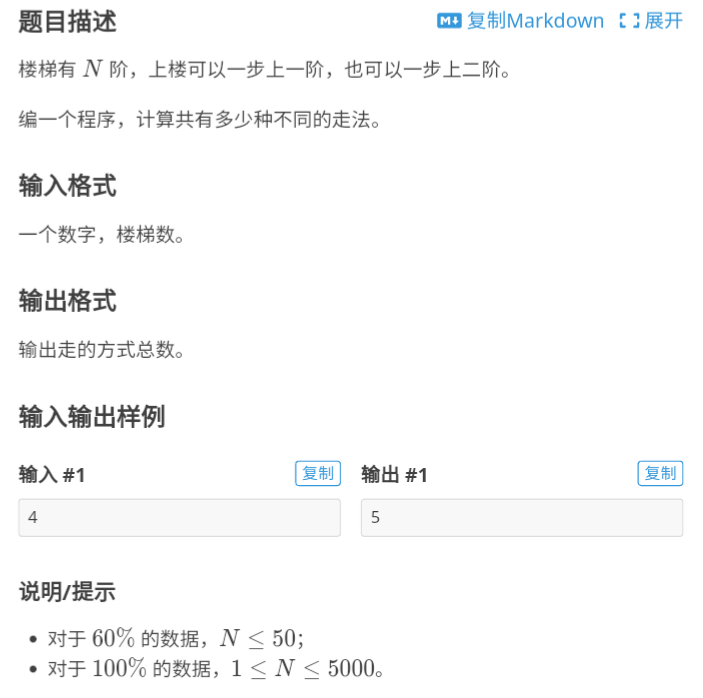        这道题一眼望去即可看出，这是一道非常简单的递推题，先列出状态转移方程：f[i] = f[i-1] + f[i-2]，f[1]=1，f[2]=2，但是再看一眼数据范围，这开long long都不够！只能用高精度，代码如下：

#include <bits/stdc++.h>

using namespace std;

int a[5010][5000],len=1,n;//a用于存放数据，其中一维是每个数据，另一维是位数，len存放最大数长度，n为楼梯阶数（循环次数）

void add(int arr){

	for(int i=1;i<=len;i++) a[arr][i]=a[arr-1][i]+a[arr-2][i];

	for(int i=1;i<=len;i++) if(a[arr][i]>=10){

		a[arr][i+1]+=a[arr][i]/10;

		a[arr][i]%=10;

	}//进位

	if(a[arr][len+1]>0) len++;//判断位数增加

	return ;

}

int main(){

	scanf("%d",&n);

	a[0][1]=1;

	a[1][1]=1;//初始化状态

	for(int i=2;i<=n;i++) add(i);//循环计算

	for(int i=len;i>0;i--) printf("%d",a[n][i]);//从高位起倒序输出

	return 0;

}

结语

        高精度是一种非常常用的计算手段，其原理就是模拟竖式计算。我是faryou，再见！

本文链接：https://blog.faryou.eu.org/post/98.html 转载需经作者授权！