前言
今天我们学习另一种DP——区间DP。

程序设计思路
（由于无法从概念上描述题意，这里直接放题目~）

题意很好理解，要求我们求出合并所有石堆的最小代价。
首先思考一维DP式，很容易想到将dp[i]定义为合并从第一堆石子到第i堆石子所花费的代价。但是，状态转移方程怎么办？！由于本题中合并的顺序不唯一，第一堆石子也有可能最后合并，所以这个方法不可行。
这个时候我们需要思考一下：某个区间的最小代价一定是这个区间分为2个区间后这两个区间的代价之和。这样我们可以得到二维DP的定义：dpi代表从第i堆到第j堆石子合并所需要的最小代价。然后再思考，不难得到：我们可以对某个区间进行分割，这个分割点就是我们要去找的。故我们可以列出以下方程：dpi=min(dpi,dpi+dpi+k+1+s[j]-s[i-1]（s[i]为从第一堆石子到第i堆石子代价的前缀和，用来累加代价，自行理解，另外需要预处理）。最后一个问题：dpi如何初始化？首先如果只有一堆那合并的代价为0，故dpi=0，而由于我们求最小代价，dp[i]j可以初始化成一个很大的数，方便比较操作。

代码实现

#include <stdio.h>
#include <memory.h>
//今天想重温一下C语言，故用C语言
int n,m[1001],dp[1001][1001],s[1001];//均如题意或已讲解

int min(int a,int b){//C语言没有min函数，所以手搓一个
    if(a<b) return a;
    else return b;
}

main(){
    scanf("%d",&n);
    memset(s,0,sizeof(s));
    memset(dp,0x3f3f3f3f,sizeof(dp));//初始化为大数
    for(int i=1;i<=n;i++) dp[i][i]=0;
    for(int i=1;i<=n;i++) scanf("%d",&m[i]);
    for(int i=1;i<=n;i++) s[i]=m[i]+s[i-1];//计算前缀和
    for(int len=1;len<=n;len++) for(int i=1;i<=n;i++){//len为长度，先计算长度为1的区间之后逐渐累加并重叠
        int j=i+len-1;
        if(j>n) break;//防越界
        for(int k=0;k<len;k++) dp[i][j]=min(dp[i][j],dp[i][i+k]+dp[i+k+1][j]+s[j]-s[i-1]);//dp式
    }
    printf("%d",dp[1][n]);
    return 0;
}

可以看到，区间DP的代码很简洁，所以重在理解~

结语
区间DP没有变式，其O(n3)的时间复杂度也无法进行优化，理解即可。我是faryou，再见！

前言
广度优先搜索适合用于解决一些走迷宫之类的问题，可以解决深度优先搜索“搜得太深一时出不来”的问题。今天我们学习一下BFS的基本思路。

程序设计思路
BFS与DFS不同就在于BFS是按照层次遍历（在树上表现为从上到下一层一层，横向遍历），而DFS则是有多深走多深，不管层数。理论上来说，两者都属于暴力。
BFS通过队列实现，即每次从队列中取出一个点进行相关操作，并在这次循环内察看其子节点是不是叶子节点，如果是非叶子节点就把这个点入队，之后将这个父节点出队，处理下一个点，直到处理完所有节点（队列空），实现遍历。
还是下面这棵树：

使用BFS的遍历顺序为：2→7→8→1→6→9→5→3→4。

代码实现
来看一道题：

这是一道经典的BFS题目，我们可以将马不同的行走路线看成一棵树上不同的分支。直接上代码——

#include <bits/stdc++.h>
using namespace std;

int n,m,x,y,ans[401][401],ssb[9]={0,-2,-2,-1,-1,2,2,1,1},sbb[9]={0,-1,1,-2,2,-1,1,-2,2},iq,aq;//n、m、x、y如题意，ans存放从起点到各个点的最短路径，iq、aq为临时变量
bool visit[401][401];//记录当前点有没有访问过

int main(){
    queue<int> f1,f2;//队列，分别记录f1与f2
    scanf("%d%d%d%d",&n,&m,&x,&y);
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) ans[i][j]=-1;
    f1.push(x);
    f2.push(y);//先将起点入队，开始计算
    ans[x][y]=0;//起点到起点距离为0
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) visit[i][j]=false;//初始化
    visit[x][y]=true;//已经访问过起点
    while(!f1.empty()){//循环直到队列空
        iq=f1.front();
        aq=f2.front();//取出x、y分别计算
        f1.pop();
        f2.pop();//出队
        for(int i=1;i<=8;i++){//马下一步可以到八个方向
            int nexx=iq+ssb[i];
            int nexy=aq+sbb[i];//临时变量记录
            if(nexx>0 && nexy>0 && nexx<=n && nexy<=m && !visit[nexx][nexy]){//判断是否超界或访问过
                visit[nexx][nexy]=true;//当前点标记
                ans[nexx][nexy]=ans[iq][aq]+1;
                f1.push(nexx);
                f2.push(nexy);//进队列
            }
        }
    }
    for(int i=1;i<=n;i++){//输出
        for(int j=1;j<=m;j++) printf("%-5d",ans[i][j]);
        printf("\n");
    }
    return 0;
}

再来看下面这题：

这题可以视作遍历二叉树，即上楼和下楼分别为节点。看代码：

#include <bits/stdc++.h>
using namespace std;

struct node{//floor存放一层，d存放到该层的步数
    int floor,d;
}now;

int n,a,b,k[201],dist;//n、a、b、k如题意，dist为临时变量
bool vis[201];//记录是否到达
queue<node> iq;//队列

int main(){
    scanf("%d%d%d",&n,&a,&b);
    for(int i=1;i<=n;i++){
        scanf("%d",&k[i]);
        vis[i]=false;
    }//初始化+读入
    iq.push((node){a,0});//起点入队
    vis[a]=true;//起点已访问过
    while(!iq.empty()){//循环直到队列空
        now=iq.front();//存放这次循环要处理的点
        iq.pop();//出队
        if(now.floor==b) break;//当已经到达终点时，退出循环。由于广搜可以保证搜索的步数逐渐增加，所以不会漏掉步数更少的情况
        dist=now.floor-k[now.floor];//临时记录（下楼）
        if(dist>=1 && dist<=n && !vis[dist]){//判断未超界且未访问过
            iq.push((node{dist,now.d+1}));//入队
            vis[dist]=1;//标记
        }
        dist=now.floor+k[now.floor];//临时记录（上楼）
        if(dist>=1 && dist<=n && !vis[dist]){//同上
            iq.push((node{dist,now.d+1}));
            vis[dist]=1;
        }
    }
    if(now.floor==b) printf("%d",now.d);
    else printf("-1");
    return 0;
}

这里注意不要忘记开vis数组，否则可能会死循环（出现环状结构时）。

结语
BFS是很重要的一个算法，只要想清楚自己的树是怎么样的就可以轻松完成程序。我是faryou，再见！

前言
搜索是算法学习者经常会用的一种算法，本质上是暴力算法的一种优化。我们在初期经常会用到BFS和DFS。今天我们来学习DFS。

什么是递归
简单来说，就是函数自己调用自己。因为函数在运行过程中产生的数据通常是存放在栈中的，所以它可以在递归开始返回后将最后一次入栈的数据出栈，再回到上一个程序。来看一个具体的例子：

本题很简单，但是也可以不用循环做，可以使用递归：

#include <bits/stdc++.h>

int times(int n){//递归程序
    if(n==1) return 1;
    else return n*times(n-1);//自己调用自己
}

int main(){
    int n;
    scanf("%d",&n);
    printf("%d",times(n));
    return 0;
}

这里程序在函数中不断调用自己，直到n=1时开始回归，巧妙的实现了从1乘到n。
需要注意的是，递归在使用过程中会有损耗，故在时间复杂度相同时会慢于普通循环。

程序设计思路
首先我们要明白搜索都是基于树论的。你想要使用搜索，就必须先自己构造出一棵树。

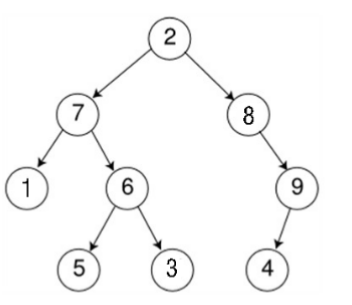
如上图所示，就是一棵树的图形表示。
与BFS不同，DFS的原则是“不撞南墙不回头”，因此如果使用DFS对上面的树进行搜索，顺序应该是：2→7→1→6→5→3→8→9→4。
由于图片中展示的是一棵二叉树，而实际问题中树的子树数量不是固定的，所以通常会使用递归的方式写程序。

代码实现
下面是一个例子：

这是一道典型的DFS的题目。在这题中，由于两个皇后肯定不会在同一行，我们可以对每一行可能出现的情况进行枚举，再进行判断。于是问题就变成了要遍历n棵n叉树并判断。下面是代码——

#include <bits/stdc++.h>
using namespace std;

int n,ans=0,out[14];//ans用于累加，out数组存放要输出的答案
bool flag;//用于记录是否有答案

void dfs(int step){//step为行数
    if(step>n){//出口程序
        ans++;
        if(ans<=3){//输出前三个答案
            for(int i=1;i<=n;i++) printf("%d ",out[i]);
            printf("\n");
        }
    }
    for(int i=1;i<=n;i++){
        flag=true;//初始化flag
        for(int j=1;j<step;j++) if(out[j]==i || abs(i-out[j])==step-j){//前一个条件判断纵向，后一个条件判断是否处于同一45°角上。
            flag=false;//当不满足条件时，将答案标记为错误并直接跳出循环不再判断（剪枝）
            break;
        }//用之前放置的所有皇后进行判断
        if(!flag)continue;//当答案不正确时，进入下一循环
        out[step]=i;//存下答案
        dfs(step+1);//进行下一层判断
    }
    return ;
}

int main(){
    scanf("%d",&n);
    dfs(1);
    printf("%d",ans);
    return 0;
}

这里我们使用递归不断调用自己，达到一个函数搞定的效果。再来看一个例子：

这题也是经典的地图搜索题，上代码：

#include <bits/stdc++.h>

int r,c,n,a,b,iq[1010];//r、c、n如题意，a、b用来存放起点坐标，iq[i]为第i次操作的方向编号（1、2、3、4分别代表东、南、西、北）
char Map[55][55],input[6];//Map用于存地图，input用来输出操作的内容
bool ans[55][55],flag[55][55][1010];//ans存放能否到达坐标对应点，flag[i][j][k]存放是否在第k步到达(i,j)（记忆化）
void dfs(int num,int x,int y){//num代表递归层数，x、y代表要进行搜索的坐标
    if(flag[x][y][num]) return ;//如果当前点已经算过则返回
    if(num>=n){//当层数大于步数时退出计算
        ans[x][y]=true;
        return ;
    }//以下为分类讨论
    int i=x,j=y;
    if(iq[num]==1) while(1){//当下一步向东走时，横坐标不断加1直到超界或撞墙
        j++;//一步一步走
        if(j>=c || Map[x][j]=='X') break;//判断超界或撞墙
        dfs(num+1,x,j);//计算下一步
    }
    if(iq[num]==2) while(1){//同上
        i++;
        if(i>=r || Map[i][y]=='X') break;
        dfs(num+1,i,y);
    }
    if(iq[num]==3) while(1){//同上
        j--;
        if(j<0 || Map[x][j]=='X') break;
        dfs(num+1,x,j);
    }
    if(iq[num]==4) while(1){//同上
        i--;
        if(i<0 || Map[i][y]=='X') break;
        dfs(num+1,i,y);
    }
    flag[x][y][num]=true;//将当前位置标记为已走过
    return ;
}

int main(){
    scanf("%d%d",&r,&c);
    for(int i=0;i<r;i++) for(int j=0;j<c;j++) ans[i][j]=false;
    for(int i=0;i<r;i++) scanf("%s",Map[i]);
    for(int i=0;i<r;i++) for(int j=0;j<c;j++) if(Map[i][j]=='*'){
        a=i;
        b=j;
    }
    scanf("%d",&n);
    for(int i=0;i<r;i++) for(int j=0;j<c;j++) for(int k=0;k<n;k++) flag[i][j][k]=false;
    for(int i=0;i<n;i++){//每读入一个操作就转义为数字操作编号
        scanf("%s",input);
        if(input[0]=='E') iq[i]=1;
        if(input[0]=='S') iq[i]=2;
        if(input[0]=='W') iq[i]=3;
        if(input[0]=='N') iq[i]=4;
    }
    dfs(0,a,b);//从(a,b)出发
    for(int i=0;i<r;i++){//输出
        for(int j=0;j<c;j++){
            if(Map[i][j]=='X') printf("X");
            else if(ans[i][j]) printf("*");//如果该点可以到达，输出'*'
            else printf(".");
        }
        printf("\n");
    }
    return 0;
}

这题要我们对地图进行计算，还是很好理解的。这里我加上了记忆化，效率更高。

DFS的优化——剪枝
剪枝，顾名思义，就是通过程序方法直接排除一些子树，以求提高效率。主要分为可行性剪枝和奇偶性剪枝。
可行性剪枝，就是从题目意义上将某些不可能的情况排除。比如说，要计算一个人能不能在规定时间刚刚好走到某个格子（路线不能重复），如果你在搜索的过程中碰到一种情况：这张地图上所有格子的总数比单位时间内可以走的路程还要少，那根本就不用算了，直接false！
还有一种奇偶性剪枝。我们可以将一张地图看成这样：
0 1 0 1 0 1 0 1

1 0 1 0 1 0 1 0

0 1 0 1 0 1 0 1

1 0 1 0 1 0 1 0

0 1 0 1 0 1 0 1

1 0 1 0 1 0 1 0

0 1 0 1 0 1 0 1

1 0 1 0 1 0 1 0
在这张图上，从0走到1或从1走到0肯定要奇数步，从0走到0或从1走到1肯定要偶数步。所以如果碰到这种平面图算步数的搜索题也可以直接用奇偶性pass一部分。
剪枝的具体代码可以是多样化的，但是其中心目的只有一个——减少搜索量。

记忆化DFS
DFS在调用的递归嵌套过多时会爆栈，因此我们可以为其加上记忆化以防超界。记忆化是指在一棵树中，可能会有重复的子树，导致重复计算，所以我们可以使用数组将一种情况记录下来，下次再碰到这个情况直接跳过计算，以减少调用。
记忆化DFS是一种以更高的空间复杂度换取更低的时间复杂度的方法。当代码面临TLE时，不妨试试加上记忆化。例如上面案例中的第二题就是利用了flag数组，减少了运算量。当然，在加记忆化时也要注意空间复杂度不能过高，否则爆空间~

总结
从理论上来说，DFS和DP问题是可以互相转化的，只要学好一个，两者的问题都能解决。所以，如果你还在为了列出状态转移方程而苦恼，不妨试试用DFS的思路去思考DP问题。不过，普通的DFS容易因循环过多而爆栈，为了解决这个问题，我们需要用到优化版DFS——记忆化DFS。我是faryou，再见！

前言
最短路径是求在一张有向图中，起点到终点的距离。求最短路径的方法有很多，如SPFA、floyd、dijkstra等，今天我们学习dijkstra的思路与代码，其优点是时间复杂度和空间复杂度都很低，缺点是不能处理重边。

程序设计思路
dijkstra基于贪心实现，又有点类似DP，其思路大致如下：先把起点到所有点的距离都设为inf（一个很大的数），然后在所有与起点相连接的边中找到最短的一条，将这个新的点作为起点，并更新从起点出发到这个点的最短距离，直到找到终点。这个逐步更新的操作被称为松弛。

代码实现

洛谷上还有一道数据随机的模板题，这题专卡SPFA，但对我们的dijskla没有影响，下面是代码：

#include <bits/stdc++.h>
#define inf 2147483647
using namespace std;

struct Edge{//结构体用来存一条边的起点、终点、长度
    int to,dis,ne;
}edge[2000005];

int n,m,s,cnt,dist[2000005],head[2000005],x,y,z;//n、m、s如题意，cnt用来计数，dist存起点到各个点的最短距离
bool visit[2000005];//类似BFS中记录已经访问的点

void Add_edge(int from,int to,int w){//加入数组
    edge[++cnt].to=to;
    edge[cnt].dis=w;
    edge[cnt].ne=head[from];
    head[from]=cnt;
}

struct node{
    int id,dis;
    bool operator <(const node &a)const{ return a.dis<dis; }//优先队列升序排序
};
void dijkstra(){
    priority_queue<node> q;
    q.push(node{s,0});
    for(int i=1;i<=n;i++) dist[i]=inf;
    dist[s]=0;
    while(!q.empty()){
        node a=q.top();
        q.pop();//类似BFS的队列
        int now=a.id;
        if(visit[now]) continue;
        visit[now]=1;
        for(int i=head[now];i;i=edge[i].ne){//查所有边
            int j=edge[i].to;
            if(dist[now]+edge[i].dis<dist[j]){//判断走的这条路是不是比原来的更短
                dist[j]=dist[now]+edge[i].dis;
                q.push(node{j,dist[j]});
            }
        }
    }
}

int main(){
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&x,&y,&z);
        Add_edge(x,y,z);
    }
    dijkstra();
    for(int i=1;i<=n;i++) printf("%d ",dist[i]);
    return 0;
}

结语
dijkstra不能处理重边，这一点在选择方法时需要注意。我是faryou，再见！

前言
最小生成树是指在一个无向图内，找出一棵树，使得各个结点之间能够互相到达，且总路径长度最短。

程序设计思路
最小生成树主要有两种思路——Kruskal和Prim，两者的时间复杂度为On2和On3，限于篇幅原因，故进行两者的讲解，只提供Kruskal的代码。
首先讲时间复杂度较高的Prim算法（有点像dijkstra）：在图中先确定一个点，将该点加入队列，之后每次循环在与队列中的所有点连接的边中找出最短边（不得与之前已经在队列中的点相连），直到所有的点都被加入队列。
Kruskal是一种基于贪心的算法：每次在所有的边中找出最短边，判断其两端有没有与之前已经相连的点重复，直到所有点之间都已连接。因此，Kruskal需要进行排序操作。

代码实现

这里只放Kruskal的代码：

#include <bits/stdc++.h>
struct tree{//存边，x、y分别代表两个端点，z为边权
    int x,y,z;
}tr[200005];

int n,m,iq,aq,sb=0,bin[5005],ans=0;//n、m如题意，iq、aq分别临时存放路径，sb用于计数（只拿n-1条边），bin存放每个点的路径，ans累加长度

int find(int a){//由于Kruskal基于树进行，可以使用路径压缩，详见并查集那篇文章
    int x=a;
    if(bin[x]!=x) return bin[x]=find(bin[x]);
    else return x;
}

bool cmp(tree a,tree b){//sort升序
    return a.z<b.z;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){//读入
        scanf("%d%d%d",&tr[i].x,&tr[i].y,&tr[i].z);
        bin[tr[i].x]=tr[i].x;
        bin[tr[i].y]=tr[i].y;
    }
    sort(tr+1,tr+m+1,cmp);//升序排序
    for(int i=1;i<=m;i++){//遍历每条边
        iq=find(tr[i].x);//找当前边的x是否连入图中
        aq=find(tr[i].y);//找当前边的y是否连入图中
        if(iq==aq) continue;//当两者祖先相同时，直接跳过防止成环
        ans+=tr[i].z;//累加
        sb++;//计次
        bin[aq]=iq;//修改路径
        if(sb==n-1) break;//当要取的边数量足够时，退出循环
    }
    for(int i=1;i<n;i++) if(find(i)!=find(i+1)){//判断每个点的祖先是否相同
        printf("orz");
        return 0;
    }
    printf("%d",ans);
    return 0;
}

这里需要注意的是，由于我们已经完成了排序，故不需要在之后判断大小。

结语
本文中讲了Kruskal的思路及代码，并融入了并查集的知识。我是faryou，再见！