前言
广度优先搜索适合用于解决一些走迷宫之类的问题，可以解决深度优先搜索“搜得太深一时出不来”的问题。今天我们学习一下BFS的基本思路。

程序设计思路
BFS与DFS不同就在于BFS是按照层次遍历（在树上表现为从上到下一层一层，横向遍历），而DFS则是有多深走多深，不管层数。理论上来说，两者都属于暴力。
BFS通过队列实现，即每次从队列中取出一个点进行相关操作，并在这次循环内察看其子节点是不是叶子节点，如果是非叶子节点就把这个点入队，之后将这个父节点出队，处理下一个点，直到处理完所有节点（队列空），实现遍历。
还是下面这棵树：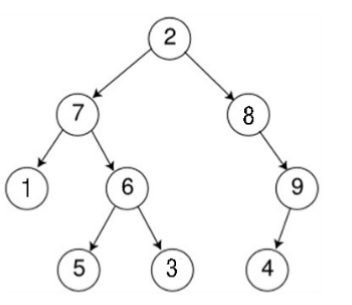

使用BFS的遍历顺序为：2→7→8→1→6→9→5→3→4。

代码实现
来看一道题：

这是一道经典的BFS题目，我们可以将马不同的行走路线看成一棵树上不同的分支。直接上代码——

#include <bits/stdc++.h>
using namespace std;

int n,m,x,y,ans[401][401],ssb[9]={0,-2,-2,-1,-1,2,2,1,1},sbb[9]={0,-1,1,-2,2,-1,1,-2,2},iq,aq;//n、m、x、y如题意，ans存放从起点到各个点的最短路径，iq、aq为临时变量
bool visit[401][401];//记录当前点有没有访问过

int main(){
    queue<int> f1,f2;//队列，分别记录f1与f2
    scanf("%d%d%d%d",&n,&m,&x,&y);
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) ans[i][j]=-1;
    f1.push(x);
    f2.push(y);//先将起点入队，开始计算
    ans[x][y]=0;//起点到起点距离为0
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) visit[i][j]=false;//初始化
    visit[x][y]=true;//已经访问过起点
    while(!f1.empty()){//循环直到队列空
        iq=f1.front();
        aq=f2.front();//取出x、y分别计算
        f1.pop();
        f2.pop();//出队
        for(int i=1;i<=8;i++){//马下一步可以到八个方向
            int nexx=iq+ssb[i];
            int nexy=aq+sbb[i];//临时变量记录
            if(nexx>0 && nexy>0 && nexx<=n && nexy<=m && !visit[nexx][nexy]){//判断是否超界或访问过
                visit[nexx][nexy]=true;//当前点标记
                ans[nexx][nexy]=ans[iq][aq]+1;
                f1.push(nexx);
                f2.push(nexy);//进队列
            }
        }
    }
    for(int i=1;i<=n;i++){//输出
        for(int j=1;j<=m;j++) printf("%-5d",ans[i][j]);
        printf("\n");
    }
    return 0;
}

再来看下面这题：

这题可以视作遍历二叉树，即上楼和下楼分别为节点。看代码：

#include <bits/stdc++.h>
using namespace std;

struct node{//floor存放一层，d存放到该层的步数
    int floor,d;
}now;

int n,a,b,k[201],dist;//n、a、b、k如题意，dist为临时变量
bool vis[201];//记录是否到达
queue<node> iq;//队列

int main(){
    scanf("%d%d%d",&n,&a,&b);
    for(int i=1;i<=n;i++){
        scanf("%d",&k[i]);
        vis[i]=false;
    }//初始化+读入
    iq.push((node){a,0});//起点入队
    vis[a]=true;//起点已访问过
    while(!iq.empty()){//循环直到队列空
        now=iq.front();//存放这次循环要处理的点
        iq.pop();//出队
        if(now.floor==b) break;//当已经到达终点时，退出循环。由于广搜可以保证搜索的步数逐渐增加，所以不会漏掉步数更少的情况
        dist=now.floor-k[now.floor];//临时记录（下楼）
        if(dist>=1 && dist<=n && !vis[dist]){//判断未超界且未访问过
            iq.push((node{dist,now.d+1}));//入队
            vis[dist]=1;//标记
        }
        dist=now.floor+k[now.floor];//临时记录（上楼）
        if(dist>=1 && dist<=n && !vis[dist]){//同上
            iq.push((node{dist,now.d+1}));
            vis[dist]=1;
        }
    }
    if(now.floor==b) printf("%d",now.d);
    else printf("-1");
    return 0;
}

这里注意不要忘记开vis数组，否则可能会死循环（出现环状结构时）。

结语
BFS是很重要的一个算法，只要想清楚自己的树是怎么样的就可以轻松完成程序。我是faryou，再见！