前言
贪心是算法中的一个重要思想，在之后的学习中，贪心都是一种解决问题的思路。今天，我们学习贪心算法。

程序设计思路
顾名思义，贪心算法是指在每个局部都采用最优解的方法，当然，这种解法对于整体来说并不一定最优解。例如下面这个问题就是典型的贪心算法解题：
你和一群硕鼠做交易，你要买12斤苹果，而以下三只硕鼠开出了三个价格，请你选择最优的方案：
第一只硕鼠：共有20斤苹果，其中4斤7元；
第二只硕鼠：共有10斤苹果，其中2斤3元；
第三只硕鼠：共有15斤苹果，其中5斤8元。
以上是一个很简单的贪心问题“硕鼠的交易”。很显然，我们要选择单价最为便宜的第二只硕鼠的单价进行交易，但因为第二只硕鼠总共只有10斤苹果，因此我们在买完了第二只硕鼠的苹果之后还需要再买价格第二便宜的第三只硕鼠的2斤苹果。

代码实现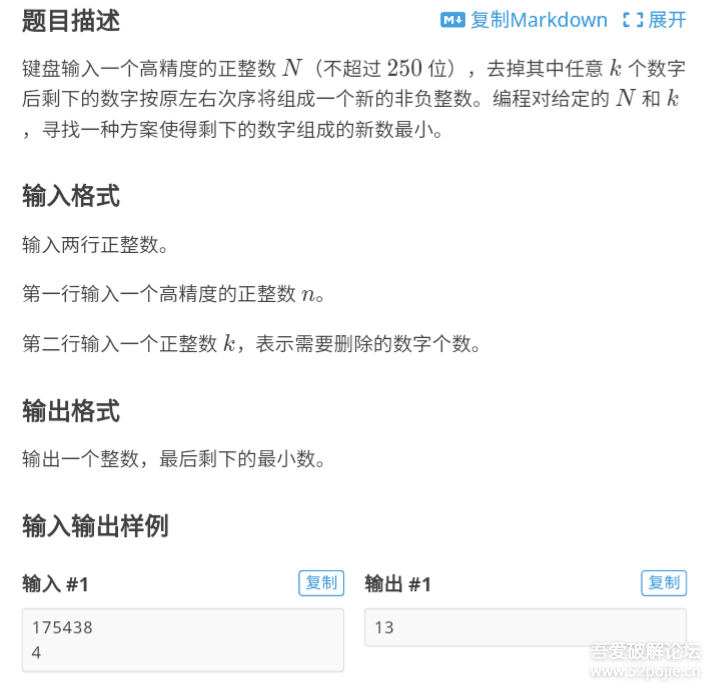

这题名叫删数问题。讲一下思路：因为要删到最小数，所以可以从左到右依次判断，如果左侧数大于右侧数，则删左侧数。之后继续判断。如果最后一个数最大，则删这个数。这种做法的思路就是使高位数小，整个数便也小了。这是贪心的思想。下面是代码实现：

#include <bits/stdc++.h>//定义头文件
using namespace std;
//说明：本人比较喜欢C风格的程序，因此没怎么涉及到C++的特性（如cout、cin、string等）
//by:faryou
char n[255];//因为位数很多，长整型显然无法存下250位，故使用字符串
int k,num=0,i=0;//k对应题目中的k，num为记录变量（记录剩余的位数，可以理解为右指针），i为指针（记录判断到的位数）
void del(int c){//删数函数，原理是将被删数右侧每一位都往左移动一位
    for(int i=c;i<=num;i++) n[i]=n[i+1];//将被删数右侧每一位都向左移位
    k--;//要删的数减少一个
    num--;//右指针减
}
int main(){
    scanf("%s%d",&n,&k);//读入数据
    while(n[num]!='\0') num++;//取总位数
    while(1){//死循环，之后有跳出条件
        if(k<=0) break;//当要删的数还剩0个时，结束循环
        if(n>n[i+1] && i!=num-1){//第一个条件判断前一个数大于后一个数，第二个防止超界
            del(i);//当左边数>右边数时，删左边数
            i=0;//从头开始判断
        }
        else if(n<=n[i+1] && i!=num-1) i++;//当前面条件不成立时，判断下一个数
        else if(i==num-1){//当判断到最后一个数时
            del(num-1);//删最后一个数
            i=0;//从头开始判
        }
    }
    while(n[0]=='0') del(0);//将前缀零删去
    if(n[0]=='\0') n[0]='0';//特判，如果前面0被删光了，添一个0
    printf("%s",n);//以字符串形式输出
    return 0;//结束程序
}

说明：个人喜欢使用C风格，因此此处使用了char数组存储数据，而且这里char比string方便（char数组末尾有'\0'做结束标识符，不需要再开一个变量存剩余位数，再拿for循环输出）。

总结
贪心算法本身不难，就是在某些解题思路上要大胆一些（多贪心）。在编写C++程序时，使用C风格也是一个不错的选择。我是faryou，再见！

前言
有时候，我们需要对数组进行排序，而在算法中，由于对效率的追求，选择排序和冒泡排序已经无法满足我们的需求。这时，我们就需要使用效率更高的快排。

程序设计思路
在快速排序中，我们需要两个指针，分别是左指针和右指针,即left和right。他们从数组两端出发，相向而行。之后找到中点，作为基准数，比基准数大的和小的各自到一边（为讲解方便，这里讲升序）。当左右指针相遇时，我们已经将所有的数分为两组。之后，我们再次进行相同操作，直到将所有的数分组不断细化，最后每个数一组。
这样一来，我们不难想到递归。即当主程序结束后，我们对两组数再次调用主程序本身，之后再次调用。
这种方法的时间复杂度是O(n log n)。

代码实现

void qsort(long long a[],long long left,long long right){三个参数分别为数组名、左右端点
    long long i,j,t;//i、j分别存放左右端点
    if(left>=right) return;//特判，用于最后退出程序
    int x=(left+right)/2;//取中点
    swap(a[x],a[left]);//防止重复
    t=a[left];//基准数
    i=left;
    j=right;
    while(i<j){
        while(a[j]>=t && i<j) j--;//j不断向左，直到发现小数
        while(a[i]<=t && i<j) i++;//i不断向右，直到发现大数
        if(i<j) swap(a[i],a[j]);//如果i比j小，交换
        else break;
    }
    swap(a[left],a[i]);//调换回来
    
    //再次调用
    if(left<i) qsort(a,left,i-1);
    if(right>i) qsort(a,j+1,right);
}

sort( , , )函数使用
在C++的STL库中，有一个sort函数，可以省去我们自写快排的烦恼。
sort( , , )函数的第一个参数是数组头地址，第二个参数是数组尾地址。第三个是cmp函数名称。下面是对数组x[ ]进行排序的代码：

int k=sizeof(x)/sizeof(x[0];//获取数组长度
sort(x,x+k,);//在默认升序序情况下，无需编写cmp()函数

当我们需要对数组进行降序排序时，就需要自写cmp函数，像这样：

bool cmp(int a,int b){//int为数组数据类型
    return a>b;
}

int k=sizeof(x)/sizeof(x[0];//获取数组长度
sort(x,x+k,cmp);

sort还可以进行结构体排序，像下面这样：

bool cmp(class a,class b){
    return a.num<b.num;//降序，如需升序请将>改为<；此处对结构体中的元素num进行排序
}

sort函数的时间复杂度为O(n log n)。

结语
快排极大的提高了效率，使得程序运行速度更快，节省了时间。我是faryou，下次见！

前言
通常情况下，我们在使用程序进行幂运算时，会利用循环乘法或pow( , )解决。但对于数据非常大的情况，这样做非常影响效率，很容易导致超时。因此，快速幂应运而生。

程序设计思路
快速幂基于二进制进行。通常情况下，我们会将其封装为一个函数binpow( , )。下面举个例子说明其原理：
我们要计算3的13次方，常规做法是：用for循环使一个变量从1开始每次乘3，这里数据小，没有问题，但如果是3100000000呢（不考虑数据溢出）？这样算肯定不对。
快速幂就很好的解决了这个问题，我们可以将3的13次方分解为：
3的13次方 = 3的8次方 3的4次方 3
这样一来，我们只需要计算3的2n次方即可，即每次进行平方运算。节省了大量时间。

代码实现

int quick(int a,int b){//计算a^b
    int res = 1;//从1乘起
    while(b>0){
        if(b&1) res=res*a;//当a（二进制）的这一位是1时，乘a
        a=a*a;//计算a^2
        b>>=1;//答案的一位（二进制）解决
    }
    return res;
}

结语
快速幂在很大程度上提升了效率，使得程序速度更快。我是faryou，再见！